| |
|
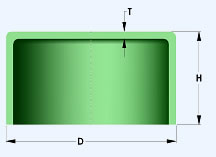
In general, the tonnage necessary to draw a shell of
round or rectangular shape is a function of the area of metal in the wall
(i.e. = mean perimeter and metal thickness). This is true because at any
given time, the force necessary to deform the metal equals the area of
metal being deformed multiplied by the yield strength of the material.
(In calculating these forces tensile strength is used, since this will
either draw the part, push out the bottom or tear the walls). This is
generally true for parts having odd shapes, although there are other factors
involved which complicate the operation.
|
|
|
| ROUND SHELLS |
 |
TONNAGE =
Π x D x T x TENSILE STRENGTH/2000 |
|
|
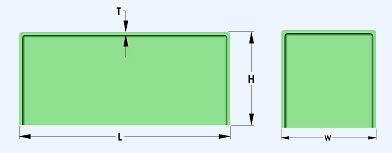
| RECTANGULAR SHELLS |
 |
TONNAGE =
2 x (L+W) x T x TENSILE STRENGTH/2000
|
|
|
Mechanical punch presses are designed
to deliver their maximum tonnage near the bottom of the stroke. Since
drawing work actually starts before bottom, the full tonnage will not
be available. The above results, therefore, should be multiplied by "G"
factor when this type press is used. |
H |
"G" |
H |
"G" |
H |
"G" |
H |
"G" |
1/2 |
1 |
3 |
1.75 |
10 |
3 |
18 |
4 |
1 |
1 |
4 |
2 |
12 |
3.25 |
20 |
4.25 |
1 1/2 |
1.5 |
6 |
2.5 |
14 |
3.5 |
22 |
4.5 |
2 |
1.5 |
8 |
2.75 |
16 |
3.75 |
24 |
4.75 |
|
Ring Holding Pressure or Force
The primary function of the draw ring is to hold the blank while it is being
formed to prevent wrinkles. Since the resistance to wrinkling becomes greater
as the metal thickness increases, the necessary R.H.F. decreases. Experience
indicates that a close approximation to the R.H.P. can be obtained by multiplying
the tonnage required to draw the shell by "J" factor (Chart 2).
Note: Disregard "G" factor for this calculation. |
|
Press Tonnage
Size of press necessary to draw shell in question is as follows:
MINIMUM PRESS TONNAGE = SHELL TONNAGE PLUS CUSHION TONNAGE (RHP)
Example
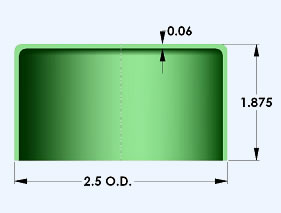
Determine the size of mechanical press required to draw the shell pictured.
|
| DRAW TONNAGE = Π x (2.50 - 0.06) x 0.06
x 55,000 / 2000 = 12.7 T x 1.5 ("G") = 19.0 T |
| CUSHION TONNAGE =
12.7 x 0.133 ("J") = 1.7 T |
| MINIMUM MECHANICAL PRESS TONNAGE = 19.0 T
+ 1.7 T = 20.7 T |
| MINIMUM HYDRAULIC PRESS TONNAGE = 12.7 T
+ 1.7 T = 14.4 T |
|
 Dayton
Die Cushions
Dayton
Die Cushions Dayton
Die Cushions
Dayton
Die Cushions